
Función de
X en
Y: la condición de existencia asegura que de cada elemento sale alguna flecha y la de unicidad que sólo sale una.
En Matemáticas, dados dos conjuntos X e Y, una función o aplicación de X en Y es una correspondencia matemática denotada

que cumple con las siguientes dos condiciones:
- Condición de existencia: Todos los elementos de X están relacionado con elementos de Y, es decir,
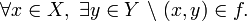
- Condición de unicidad: Cada elemento de X esta relacionado con un único elemento de Y, es decir, si

Una función es un caso particular de relación y de correspondencia matemática. Cada relación o correspondencia de un elemento  con un (y sólo un)
con un (y sólo un)  se denota
se denota  , en lugar de
, en lugar de 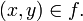
Para toda función  podemos definir:
podemos definir:
Dominio
El dominio de  es el conjunto de existencia de la misma, es decir, los elementos para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota
es el conjunto de existencia de la misma, es decir, los elementos para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota  o bien
o bien 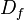 y está definido por:
y está definido por:

Recorrido o codominio
El recorrido o conjunto de llegada de  es el conjunto
es el conjunto  y se denota
y se denota  o bien
o bien 
Rango
El rango de  está formada por los valores que alcanza la misma. Es el conjunto de todos los objetos transformados, se denota
está formada por los valores que alcanza la misma. Es el conjunto de todos los objetos transformados, se denota  o bien
o bien  y está definida por:
y está definida por:

Preimagen
Una preimagen de un  es algún
es algún  tal que
tal que 
Note que  , y que algunos elementos del recorrido pueden no ser imagen de ningún elemento del dominio. En efecto, puede darse que
, y que algunos elementos del recorrido pueden no ser imagen de ningún elemento del dominio. En efecto, puede darse que  tal que
tal que 
Ejemplos
- La función definida por
 , tiene como dominio e imagen todos los números reales
, tiene como dominio e imagen todos los números reales 

Función con Dominio X y Codominio Y
- Para la función
 , en cambio, si bien su dominio es
, en cambio, si bien su dominio es  , sólo tendrá como imagen los valores comprendidos entre 0 y +∞ que sean el cuadrado de un número real.
, sólo tendrá como imagen los valores comprendidos entre 0 y +∞ que sean el cuadrado de un número real.
- En la figura se puede apreciar una función
 , con
, con


- Note que a cada elemento de X le corresponde un único elemento de Y. Además, el elemento a de Y no tiene origen, y el elemento b tiene dos (el 1 y el 4). Finalmente,

- Esta función representada como relación, queda:

Representación de funciones
Las funciones se pueden representar de distintas maneras:
- Como expresión matemática: ecuaciones de la forma y = f(x), que permiten representar el comportamiento de la función a lo largo de todo su dominio.
- Ejemplo: y=x+2.
- Como tabulación: tabla que permite representar algunos valores discretos de la función.
- Ejemplo:
X| -2 -1 0 1 2 3
Y| 0 1 2 3 4 5
- Ejemplo: A={(-2, 0),(-1, 1),(0, 2),(1, 3), ... (x, x+2)}
- Como proposición: una descripción por comprensión de lo que hace la función.
- Ejemplo: "Para todo x, número entero, y vale x más dos unidades".
- Ejemplo:
| 5 |
|
|
|
|
|
X |
| 4 |
|
|
|
|
X |
|
| 3 |
|
|
|
X |
|
|
| 2 |
|
|
X |
|
|
|
| 1 |
|
X |
|
|
|
|
| 0 |
X |
|
|
|
|
|
| y / x |
-2 |
-1 |
0 |
1 |
2 |
3 |
Funciones según tipo de aplicación
Dados dos conjuntos X e Y, podemos clasificar a todas las funciones  definidas entre ellos, en:
definidas entre ellos, en:
Función inyectiva
Aquellas en que a cada imagen le corresponde un único origen. Formalmente,
 o lo que es lo mismo,
o lo que es lo mismo,

Función sobreyectiva Aquellas en que la aplicación es sobre todo el codominio, es decir, cuando el conjunto imagen  . Esto significa que todo elemento del codominio tiene un origen. Formalmente,
. Esto significa que todo elemento del codominio tiene un origen. Formalmente,

Estas funciones también se conocen como exhaustivas o epiyectivas.

Ejemplos

Sobreyectiva, no inyectiva |

Inyectiva, no sobreyectiva |

Biyectiva |

No sobreyectiva, no inyectiva |
Álgebra de las funciones
Composición de funciones Dadas dos funciones
f: A → B y
g: B → C, donde la
imagen de
f está contenida en el
dominio de
g, se define la función composición
(g ο f ): A → C como
(g ο f)(x) = g (f(x)), para todos los elementos
x de
A.


Función identidad
Dado un conjunto  , la función
, la función  que asigna a cada
que asigna a cada  de
de  el mismo
el mismo  de
de  se denomina función identidad o función unitaria.
se denomina función identidad o función unitaria.

Dada cualquier función  , es claro que
, es claro que  es igual a
es igual a  y que
y que  es también igual a
es también igual a  , puesto que para todo
, puesto que para todo  y también
y también 

Función inversa
Dada una función  , se denomina función inversa de
, se denomina función inversa de  ,
,  a la función que cumple la siguiente condición:
a la función que cumple la siguiente condición:


Si existe una función que cumpla esas dos condiciones, ser inversa por la izquierda y ser inversa por la derecha, se demuestra que esa función es única. Eso justifica la notación 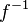 , que sería ambigua si pudiera haber dos inversas de la misma función.
, que sería ambigua si pudiera haber dos inversas de la misma función.
Sólo algunas funciones tienen inversa. De hecho, la condición necesaria y suficiente para la existencia de 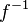 es que
es que  sea biyectiva. Por tanto, las afirmaciones
sea biyectiva. Por tanto, las afirmaciones
- Existe función inversa de
 y
y
 es biyectiva
es biyectiva
son lógicamente equivalentes.
El grupo de las funciones biyectivas
Considerando todas las funciones biyectivas  , las conclusiones del apartado anterior pueden resumirse en:
, las conclusiones del apartado anterior pueden resumirse en:
- Dadas tres funciones la operación de composición es asociativa:

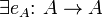 tal que
tal que  tenemos
tenemos 

Estas tres condiciones determinan un grupo. El conjunto de las funciones biyectivas  es un grupo con respecto a la operación de composición de funciones y recibe el nombre de grupo simétrico de
es un grupo con respecto a la operación de composición de funciones y recibe el nombre de grupo simétrico de  .
.



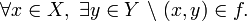

 con un (y sólo un)
con un (y sólo un)  se denota
se denota  , en lugar de
, en lugar de 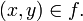
 es el conjunto de existencia de la misma, es decir, los elementos para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota
es el conjunto de existencia de la misma, es decir, los elementos para los cuales la función está definida. Es el conjunto de todos los objetos que puede transformar, se denota  o bien
o bien 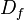 y está definido por:
y está definido por:
 y se denota
y se denota  o bien
o bien 
 o bien
o bien  y está definida por:
y está definida por:

 , y que algunos elementos del recorrido pueden no ser imagen de ningún elemento del dominio. En efecto, puede darse que
, y que algunos elementos del recorrido pueden no ser imagen de ningún elemento del dominio. En efecto, puede darse que  tal que
tal que 
 , tiene como dominio e imagen todos los
, tiene como dominio e imagen todos los 

 , en cambio, si bien su dominio es
, en cambio, si bien su dominio es  , sólo tendrá como imagen los valores comprendidos entre 0 y +
, sólo tendrá como imagen los valores comprendidos entre 0 y +



 o lo que es lo mismo,
o lo que es lo mismo, 
 . Esto significa que todo elemento del codominio tiene un origen. Formalmente,
. Esto significa que todo elemento del codominio tiene un origen. Formalmente,







 , la función
, la función  que asigna a cada
que asigna a cada  de
de  el mismo
el mismo 
 , es claro que
, es claro que  es igual a
es igual a  es también igual a
es también igual a  y también
y también 

 , se denomina función inversa de
, se denomina función inversa de  ,
,  a la función que cumple la siguiente condición:
a la función que cumple la siguiente condición:

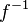 , que sería ambigua si pudiera haber dos inversas de la misma función.
, que sería ambigua si pudiera haber dos inversas de la misma función. , las conclusiones del apartado anterior pueden resumirse en:
, las conclusiones del apartado anterior pueden resumirse en:
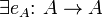 tal que
tal que  tenemos
tenemos 

 es un grupo con respecto a la operación de composición de funciones y recibe el nombre de grupo simétrico de
es un grupo con respecto a la operación de composición de funciones y recibe el nombre de grupo simétrico de