La teoría de conjuntos es una división de las matemáticas que estudia los conjuntos . El primer estudio formal sobre el tema fue realizado por el matemático alemán Georg Cantor en el Siglo XIX y más tarde reformulada por Zermelo.
Conceptos básicos [editar]

Diagrama de Venn que muestra un conjunto
A contenido en otro conjunto
U y su diferencia
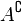
El concepto de conjunto es intuitivo y podríamos definirlo simplemente como una colección de objetos, así podemos hablar de un conjunto de personas, ciudades, lapiceros o del conjunto de objetos que hay en un momento dado encima de una mesa. Un conjunto esta bien definido si se sabe si un determinado elemento pertenece o no al conjunto, así el conjunto de los bolígrafos azules, esta bien definido, porque a la vista de un bolígrafo podemos saber si es azul o no. El conjunto de las personas altas no esta bien definido, porque a la vista de una persona, no siempre podrá decir si es alta o no, o puede haber distintas personas, que opinen si esa persona es alta o no lo es.
En el siglo XIX segun Frege; los elementos de un conjunto se definían sólo por tal o cual propiedad. Actualmente la teoría de conjuntos está bien definida por el sistema ZFC, sin embargo sigue siendo célebre la definición que publicó Cantor
Se entiende por conjunto a la agrupación en un todo de objetos bien diferenciados de nuestra intuición o nuestra mente.
El diagrama que muestra el contenido a mano izquierda son los Diagramas de Venn que son representaciones usadas únicamente para la TEORÍA DE CONJUNTOS, estos muestran las relaciones entre diferentes gupos de cosas representando cada conjunto mediante un óvalo o círculo
Notación
Usualmente los conjuntos se representan con una letra mayúscula: A, B, K,...
Llamaremos elemento, a cada uno de los objetos que forman parte de un conjunto, estos elementos tienen carácter individual, tienen cualidades que nos permiten diferenciarlos, y cada uno de ellos es único, no habiendo elementos duplicados o repetidos. Los representaremos con una letra minúscula: a, b, k,...
De esta manera, si  es un conjunto, y
es un conjunto, y  todos sus elementos, es común escribir:
todos sus elementos, es común escribir:

para definir a tal conjunto  . Esta notación empleada para definir al conjunto
. Esta notación empleada para definir al conjunto  se llama notación por extensión
se llama notación por extensión
Para representar que un elemento  pertenece a un conjunto A, escribimos
pertenece a un conjunto A, escribimos  (léase "x en A", "x pertenece a A" o bien "x es un elemento de A"). La negación de
(léase "x en A", "x pertenece a A" o bien "x es un elemento de A"). La negación de  se escribe
se escribe 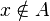 (léase
(léase  no pertenece a
no pertenece a  ).
).
El conjunto universal, que siempre representaremos con la letra U (u mayúscula), es el conjunto de todas las cosas sobre las que estemos tratando. Así, si hablamos de números enteros entonces U es el conjunto de los números enteros, si hablamos de ciudades, U es el conjunto de todas las ciudades, este conjunto universal puede mencionarse explícitamente, o en la mayoría de los casos se da por supuesto dado el contexto que estemos tratando, pero siempre es necesario demostrar la existencia de dicho conjunto previamente.
Existe además, un único conjunto que no tiene elementos al que se le llama conjunto vacío y que se denota por  . Es decir
. Es decir
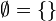
La característica importante de este conjunto es que satisface todos los elementos posibles no están contenidos en él, es decir
 .
.
Por otro lado, si todos los elementos  de un conjunto A satisfacen alguna propiedad, misma que pueda ser expresada como una proposición
de un conjunto A satisfacen alguna propiedad, misma que pueda ser expresada como una proposición  , con la indeterminada
, con la indeterminada  , usamos la notación por comprensión, y se puede definir:
, usamos la notación por comprensión, y se puede definir:

Lo anterior se lee "A es el conjunto de elementos x, que cumplen la propiedad p(x)". El símbolo ":" se lee "que cumplen la propiedad" o "tales que"; este símbolo puede ser remplazado por una barra  .
.
Por ejemplo, el conjunto  puede definirse por:
puede definirse por:

donde el símbolo  representa al conjunto de los números naturales.
representa al conjunto de los números naturales.
El uso de algún conjunto U es muy importante, ya que de no hacerlo se podría caer en contradicciones como ejemplo

Es decir, M es el conjunto donde cada elemento x satisface la propiedad  . Al principio uno podría creer que ningún conjunto puede estar contenido en sí mismo y que por lo tanto M no contiene elemento alguno; sin embargo, en vista de que M es un conjunto, cabe hacer la pregunta "¿
. Al principio uno podría creer que ningún conjunto puede estar contenido en sí mismo y que por lo tanto M no contiene elemento alguno; sin embargo, en vista de que M es un conjunto, cabe hacer la pregunta "¿ ?" Si la respuesta es negativa (
?" Si la respuesta es negativa ( ) entonces M cumple la propiedad
) entonces M cumple la propiedad  y por lo tanto
y por lo tanto  . Si por el contrario la respuesta es afirmativa (
. Si por el contrario la respuesta es afirmativa ( ), entonces M no cumple con la propiedad
), entonces M no cumple con la propiedad  y por esta razón
y por esta razón  . Esta paradoja es muy famosa y se conoce como la paradoja del barbero esta es una de las tantas incongruencias que tenía la teoría de Cantor.
. Esta paradoja es muy famosa y se conoce como la paradoja del barbero esta es una de las tantas incongruencias que tenía la teoría de Cantor.
Igualdad entre conjuntos. Subconjuntos y Superconjuntos
Igualdad de conjuntos
Dos conjuntos  y
y  se dicen iguales, lo que se escribe
se dicen iguales, lo que se escribe  si constan de los mismos elementos. Es decir, si y solo si todo elemento de A está también contenido en B y todo elemento de B está contenido en A. En símbolos:
si constan de los mismos elementos. Es decir, si y solo si todo elemento de A está también contenido en B y todo elemento de B está contenido en A. En símbolos:

Subconjuntos y Superconjuntos

Diagrama de Venn que muestra

Un conjunto  se dice que es subconjunto de otro
se dice que es subconjunto de otro  , si cada elemento de
, si cada elemento de  es también elemento de
es también elemento de  , es decir, cuando se verifique:
, es decir, cuando se verifique:
 ,
,
sea cual sea el elemento  . En tal caso, se escribe
. En tal caso, se escribe  .
.
Cabe señalar que, por definición, no se excluye la posibilidad de que si  , se cumpla
, se cumpla  . Si
. Si  tiene por lo menos un elemento que no pertenezca al conjunto
tiene por lo menos un elemento que no pertenezca al conjunto  , pero si todo elemento de
, pero si todo elemento de  es elemento de
es elemento de  , entonces decimos que
, entonces decimos que  es un subconjunto propio de
es un subconjunto propio de  , lo que se representa por
, lo que se representa por 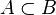 . En otras palabras,
. En otras palabras, 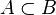 si y sólo si
si y sólo si  , y
, y  . Así, el conjunto vacío es subconjunto propio de todo conjunto (excepto de sí mismo), y todo conjunto A es subconjunto impropio de sí mismo.
. Así, el conjunto vacío es subconjunto propio de todo conjunto (excepto de sí mismo), y todo conjunto A es subconjunto impropio de sí mismo.
Si  es un subconjunto de
es un subconjunto de  , decimos también que
, decimos también que  es un superconjunto de
es un superconjunto de  , lo que se escribe
, lo que se escribe  . Así pues
. Así pues
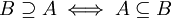 ,
,
y también que:
 ,
,
significando  que
que  es superconjunto propio de
es superconjunto propio de  .
.
Por el principio de identidad, es siempre cierto 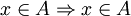 , para todo elemento
, para todo elemento  , por lo que todo conjunto es subconjunto (y también superconjunto) de sí mismo.
, por lo que todo conjunto es subconjunto (y también superconjunto) de sí mismo.
Vemos que  es una relación de orden sobre un conjunto
es una relación de orden sobre un conjunto  de conjuntos, pues
de conjuntos, pues
-
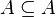 |
|
|
( es reflexiva) es reflexiva) |
 |
 |
 |
( es antisimétrica) es antisimétrica) |
 |
 |
 |
( es transitiva) es transitiva) |
Operaciones de conjuntos
Sean  y
y  dos conjuntos.
dos conjuntos.
Unión
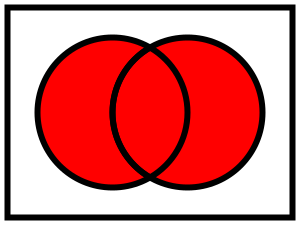
Diagrama de Venn que ilustra

Para cada par de conjuntos A y B existe un conjunto que se denota como  el cual contiene todos los elementos de A y de B. De manera más general, para cada conjunto S existe otro conjunto denotado como
el cual contiene todos los elementos de A y de B. De manera más general, para cada conjunto S existe otro conjunto denotado como  de manera que sus elementos son todos los
de manera que sus elementos son todos los  tales que
tales que  . De esta manera
. De esta manera  es el caso especial donde
es el caso especial donde  .
.
Es claro que el hecho de que un elemento x pertenezca a  es condición necesaria y suficiente para afirmar que x es un elemento de A o al menos de B. Es decir
es condición necesaria y suficiente para afirmar que x es un elemento de A o al menos de B. Es decir
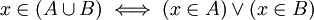
Ejemplos: si tenemos los conjuntos


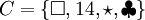

Entonces




Intersección
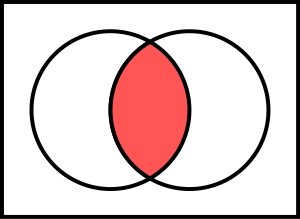
Diagrama de Venn que ilustra

Los elementos comunes a  y
y  forman un conjunto denominado intersección de
forman un conjunto denominado intersección de  y
y  , representado por
, representado por  . Es decir,
. Es decir,  es el conjunto que contiene a todos los elementos de A que al mismo tiempo están en B:
es el conjunto que contiene a todos los elementos de A que al mismo tiempo están en B:
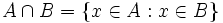 .
.
Si dos conjuntos  y
y  son tales que
son tales que 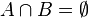 , entonces
, entonces  y
y  se dice que son conjuntos disjuntos.
se dice que son conjuntos disjuntos.
Es claro que el hecho de que 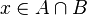 es condición necesaria y suficiente para afirmar que
es condición necesaria y suficiente para afirmar que  y
y 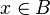 . Es decir
. Es decir

Ejemplos: si tenemos los conjuntos
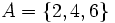


Entonces:


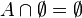

Diferencia
Los elementos de un conjunto  que no se encuentran en otro conjunto
que no se encuentran en otro conjunto  , forman otro conjunto llamado diferencia de
, forman otro conjunto llamado diferencia de  y
y  , representado por
, representado por  . Es decir:
. Es decir:
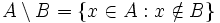 .
.
o dicho de otra manera:
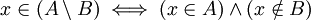
Algunas personas prefieren denotar la diferencia de  y
y  como
como  .
.
Una propiedad interesante de la diferencia es que

eso es porque
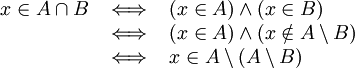
Ejemplos: Sin importar cual conjunto A elija usted, siempre se cumple



Complemento
El complemento de un conjunto A, es el conjunto de los elementos que pertenecen a algún conjunto U pero no pertenecen a A, que lo representaremos por 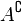 . Es decir
. Es decir

El conjunto complemento siempre lo es respecto al conjunto universal que estamos tratando, esto es, si hablamos de números enteros, y definimos el conjunto de los números pares, el conjunto complemento de los números pares, es el formado por los números no pares. Si estamos hablando de personas, y definimos el conjunto de las personas rubias, el conjunto complementario es el de las personas no rubias.
En vista de que  y
y  , entonces
, entonces
 ,
,
de manera que
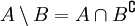
Pero también

de modo que

Diferencia simétrica
Los elementos de dos conjuntos,A y B a excepción de aquellos que se encuentran en el área de intersección de dichos conjuntos se define la diferencia simétrica.

Álgebra de conjuntos
Sean A, B, y C conjuntos cualesquiera y U un conjunto tal que  ,
,  y
y  entonces:
entonces:
-


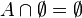
 Elemento neutro de la unión
Elemento neutro de la unión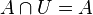 Elemento neutro de la intersección
Elemento neutro de la intersección
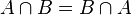 Propiedad conmutativa de la intersección
Propiedad conmutativa de la intersección Propiedad conmutativa de la unión
Propiedad conmutativa de la unión Propiedad de Involución.
Propiedad de Involución. Propiedad asociativa de la intersección
Propiedad asociativa de la intersección Propiedad asociativa de la unión
Propiedad asociativa de la unión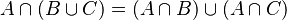 Propiedad distributiva de la intersección
Propiedad distributiva de la intersección Propiedad distributiva de la unión
Propiedad distributiva de la unión
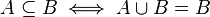

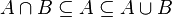
-
Producto cartesiano de conjuntos o producto cruz
Un par ordenado de números 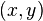 es tal si los pares
es tal si los pares 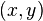 y
y  son uno mismo si y sólo si
son uno mismo si y sólo si  .
.
Dados dos conjuntos  y
y  , definimos al conjunto producto ( o producto cartesiano) de
, definimos al conjunto producto ( o producto cartesiano) de  y
y  (en ese orden), representado por
(en ese orden), representado por  , como el conjunto
, como el conjunto

- Ejemplo
- Sean
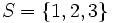 y
y  . Así,
. Así,
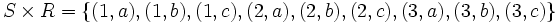
Ya que el producto cartesiano está formado de pares ordenados (donde el orden de los componentes importa), resulta

Cuantificadores
Los cuantificadores sirven para indicar cuantos elementos de un conjunto dado cumplen con cierta propiedad. Tales cuantificadores son
-
- El cuantificador universal, representado por
 . Este cuantificador se emplea para afirmar que todos los elementos de un conjunto cumplen con determinada propiedad. Se escribe
. Este cuantificador se emplea para afirmar que todos los elementos de un conjunto cumplen con determinada propiedad. Se escribe

-
- El cuantificador existencial se usa para indicar que al menos un elemento de un conjunto
 cumple con una propiedad. Se escribe
cumple con una propiedad. Se escribe
 .
.
Se definen


Funciones
Sean  y
y  dos conjuntos. Un subconjunto
dos conjuntos. Un subconjunto  , se dice aplicación o función de
, se dice aplicación o función de  en
en  , lo que se representa por
, lo que se representa por
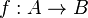
siempre que se verifique
-
Si  , el elemento
, el elemento 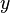 se dice imagen de
se dice imagen de  por
por  , y el elemento
, y el elemento  se llama antecedente de
se llama antecedente de 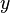 por
por  .
.
Sea una función 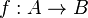 . Se emplea la notación
. Se emplea la notación  para representar a la imagen de
para representar a la imagen de  por
por  , y por tanto
, y por tanto  .
.
Sean las funciones  y
y  . Se define
. Se define
 ,
,
y se dice que  es el producto de composición de las funciones
es el producto de composición de las funciones  y
y 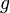 .
.
Vemos que ![fcirc (gcirc h)(x)=(gcirc h)(f(x))=hleft [g(f(x))right ],](http://upload.wikimedia.org/math/a/3/9/a399557578c46a10debaf3239907c38b.png)
y
=hleft [ (fcirc g)(x)right ]=hleft [g(f(x))right ],](http://upload.wikimedia.org/math/3/e/6/3e6b284e2886a2dafc2319669ffcd018.png)
por lo que
